4 641 Divided By 39
pachranga
Sep 09, 2025 · 6 min read
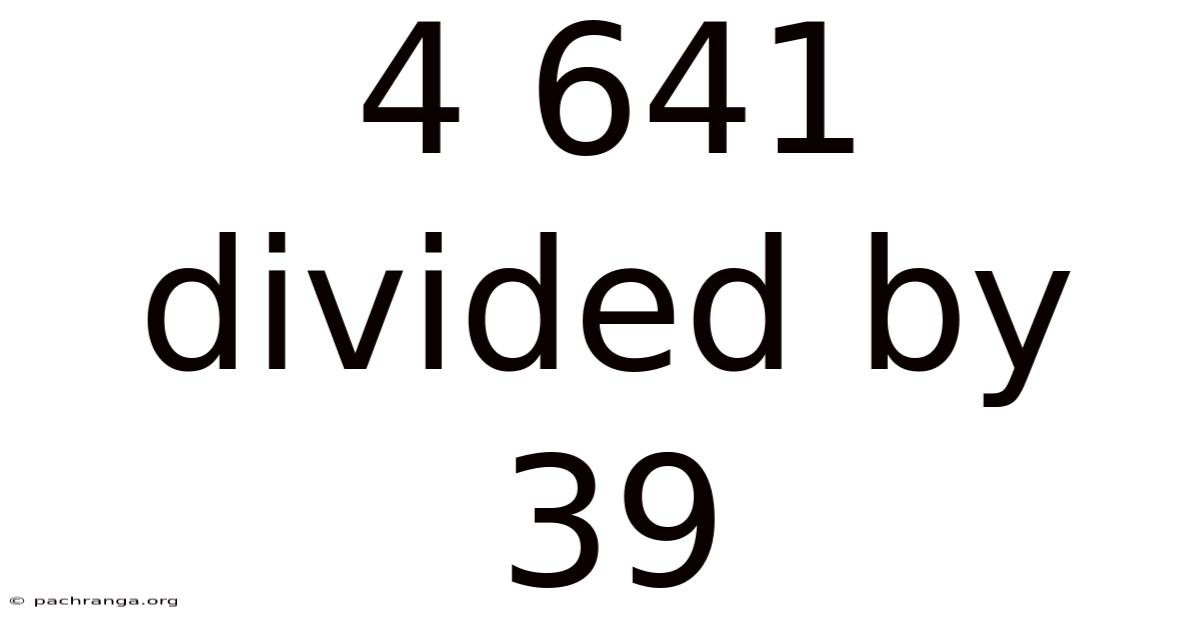
Table of Contents
Decoding the Division: A Deep Dive into 4641 Divided by 39
Dividing 4641 by 39 might seem like a simple arithmetic problem, but let's delve deeper than just the answer. This article will not only provide the solution but will explore the underlying mathematical concepts, different methods of solving the problem, and practical applications to demonstrate its relevance. Understanding this seemingly simple division problem can unlock a deeper appreciation for fundamental mathematical principles and their real-world applications.
Introduction: Understanding Division
Before we tackle 4641 ÷ 39, let's refresh our understanding of division. Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It's essentially the process of splitting a quantity into equal parts. In the context of 4641 ÷ 39, we're asking: "How many times does 39 fit into 4641?" The answer will be a quotient, representing the number of times 39 goes into 4641 evenly, and potentially a remainder, representing the amount left over.
This particular problem is a prime example of long division, a method used for dividing larger numbers where mental calculation alone becomes impractical. Long division employs a systematic approach, breaking down the division into smaller, manageable steps. Mastering long division is crucial for understanding more advanced mathematical concepts in algebra, calculus, and beyond.
Method 1: Long Division - The Classic Approach
Let's solve 4641 ÷ 39 using the traditional long division method:
119
39 | 4641
-39
---
74
-39
---
351
-351
---
0
Step-by-step explanation:
-
Divide: We start by dividing the first digit of the dividend (4641) by the divisor (39). 39 doesn't go into 4, so we consider the first two digits, 46. 39 goes into 46 once (1). We write the 1 above the 6.
-
Multiply: We multiply the quotient (1) by the divisor (39), resulting in 39.
-
Subtract: We subtract 39 from 46, giving us 7.
-
Bring down: We bring down the next digit from the dividend (4), making it 74.
-
Repeat: We repeat steps 1-4. 39 goes into 74 once (1). We write 1 above the 4. 1 x 39 = 39. Subtracting 39 from 74 gives 35.
-
Bring down: We bring down the last digit (1), making it 351.
-
Repeat: 39 goes into 351 nine times (9). We write 9 above the 1. 9 x 39 = 351. Subtracting 351 from 351 gives 0.
Therefore, 4641 ÷ 39 = 119 with a remainder of 0. This indicates that 39 divides 4641 exactly 119 times.
Method 2: Estimation and Adjustment
Long division, while reliable, can be time-consuming. An alternative approach involves estimation and iterative adjustment.
-
Estimate: We can start by estimating how many times 39 goes into 4641. Rounding 39 to 40, we can roughly estimate 4641/40 ≈ 116.
-
Adjust: Let's check if 116 is correct: 116 x 39 = 4524. This is close to 4641, but not exact.
-
Refine: The difference between 4641 and 4524 is 117. Since this is greater than 39, we know that 116 is an underestimate.
-
Iterate: Let’s try 117: 117 x 39 = 4563. The difference is 78, still too big.
-
Final Iteration: Let's try 118: 118 x 39 = 4602. The difference is 39, still not exact.
-
Solution: Finally, let's try 119: 119 x 39 = 4641. We have found the correct quotient.
This method demonstrates that through intelligent estimation and iterative refinement, we can arrive at the correct answer. Although it requires more steps than long division in this particular instance, it showcases a flexible approach to problem-solving.
The Significance of Remainders
While our problem yielded a clean result with no remainder, it's essential to understand the significance of remainders in division. A remainder indicates that the divisor does not divide the dividend exactly. This is common in real-world scenarios. For example, if you have 4641 apples and want to divide them equally among 39 people, each person would get 119 apples, and there would be no apples left over. However, if the numbers were different and resulted in a remainder, that remainder would represent the leftover apples.
Practical Applications of Division
Division is fundamental to numerous real-world applications across various fields:
-
Finance: Calculating interest rates, splitting bills, determining profit margins, and analyzing financial statements all involve division.
-
Engineering: Designing structures, calculating material requirements, and determining load capacities rely heavily on division.
-
Computer Science: Data processing, algorithm design, and memory allocation frequently use division.
-
Everyday Life: Sharing items equally among friends, calculating unit prices, measuring ingredients for recipes, and converting units all utilize the concept of division.
This specific example of 4641 ÷ 39, while seemingly simple, underlines the core principles of division that are applicable in a vast array of contexts.
Exploring Further: Prime Factorization
We can enhance our understanding by looking at the prime factorization of both 4641 and 39. Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
-
The prime factorization of 39 is 3 x 13.
-
The prime factorization of 4641 is more complex and requires methods like trial division or more advanced algorithms. It turns out that 4641 = 3 x 13 x 119.
Notice that the prime factors of 39 (3 and 13) are also factors of 4641. This explains why the division results in a whole number with no remainder. The presence of common factors simplifies the division process, and understanding prime factorization gives further insight into the mathematical relationship between the dividend and the divisor.
Frequently Asked Questions (FAQ)
Q1: What if the divisor was larger than the dividend?
A1: If the divisor (the number you're dividing by) is larger than the dividend (the number you're dividing into), the quotient is 0, and the remainder is the dividend itself. For instance, 39 ÷ 4641 would result in a quotient of 0 and a remainder of 39.
Q2: Can I use a calculator to solve this?
A2: Absolutely! Calculators are valuable tools for performing complex calculations quickly and accurately. However, understanding the underlying mathematical processes remains crucial for building a strong mathematical foundation.
Q3: Are there other methods to solve this division problem?
A3: Yes, there are alternative algorithms and computational methods for division, including synthetic division (for polynomial division), repeated subtraction, and using specialized software or programming languages. However, the methods described above provide a strong foundational understanding.
Q4: Why is it important to learn long division?
A4: While calculators are readily available, mastering long division strengthens your understanding of place value, numerical relationships, and problem-solving strategies. It forms the basis for more advanced mathematical concepts.
Conclusion: Beyond the Numbers
Solving 4641 ÷ 39 is more than just finding the quotient 119. It's about grasping the fundamental concepts of division, exploring different solution methods, and appreciating the practical relevance of this seemingly simple arithmetic operation. From financial planning to engineering design, division is a cornerstone of mathematical understanding and practical application. Mastering this fundamental skill empowers you to tackle more complex mathematical problems and strengthens your analytical thinking skills. By exploring the problem from multiple perspectives, we've not only found the solution but have also delved into the rich mathematical landscape surrounding it. This approach highlights the beauty and practicality of mathematics beyond mere calculations.
Latest Posts
Latest Posts
-
180 Cm To Ft Height
Sep 10, 2025
-
How Tall Is 42 Cm
Sep 10, 2025
-
67 Fahrenheit Convert To Celsius
Sep 10, 2025
-
7 Grados Fahrenheit A Centigrados
Sep 10, 2025
-
How Long Is 104 Cm
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 4 641 Divided By 39 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.