5 10 15 20 25
pachranga
Sep 15, 2025 · 6 min read
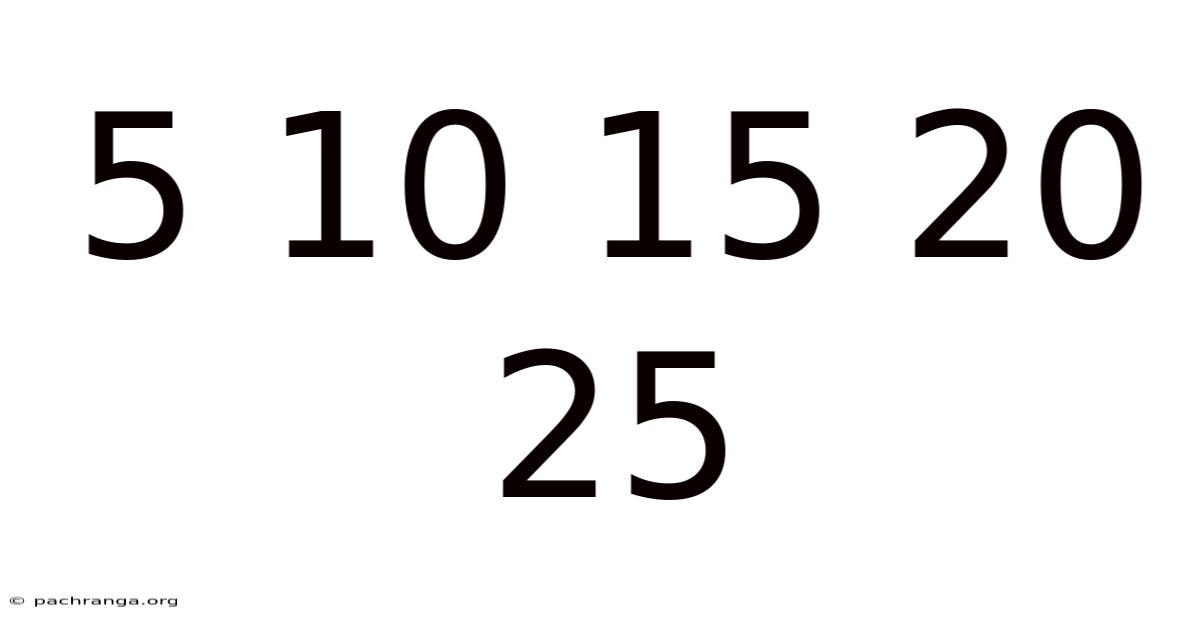
Table of Contents
Decoding the Sequence: Exploring the Mathematical and Creative Potential of 5, 10, 15, 20, 25
The seemingly simple sequence 5, 10, 15, 20, 25 might appear unremarkable at first glance. However, this arithmetic progression holds a surprising depth, revealing connections to various mathematical concepts and offering fertile ground for creative exploration. This article delves into the intricacies of this sequence, examining its mathematical underpinnings, exploring its applications in different fields, and uncovering its hidden potential for artistic and imaginative expression. Understanding this seemingly basic sequence opens doors to a deeper appreciation of mathematical patterns and their influence on our world.
Introduction: The Arithmetic Progression and its Significance
The sequence 5, 10, 15, 20, 25 is an example of an arithmetic progression – a sequence where the difference between consecutive terms remains constant. In this case, the common difference is 5. This simple characteristic underlies many of the sequence's properties and allows us to predict future terms, extrapolate backwards, and explore related mathematical concepts. The seemingly straightforward nature of arithmetic progressions belies their profound importance in mathematics, forming the basis for many more complex mathematical ideas and finding applications across diverse fields.
Understanding the Mathematical Properties
Several key mathematical properties are inherent to the sequence 5, 10, 15, 20, 25:
-
Common Difference: As mentioned earlier, the most defining characteristic is the constant difference of 5 between consecutive terms. This allows for easy prediction of subsequent terms (30, 35, 40, etc.) and the derivation of a general formula.
-
General Formula: The nth term of an arithmetic progression can be expressed using a general formula. For this sequence, the formula is:
a_n = 5n, wherea_nrepresents the nth term andnrepresents the position in the sequence (e.g., for the 4th term, n=4, and a_4 = 5*4 = 20). This formula provides a powerful tool for calculating any term within the sequence or even extrapolating far beyond the initial sequence. -
Sum of the Series: The sum of the terms in an arithmetic progression can also be calculated using a formula. For the first 'n' terms, the sum (S_n) is given by:
S_n = n/2 * (a_1 + a_n), wherea_1is the first term anda_nis the nth term. For example, the sum of the first five terms (5, 10, 15, 20, 25) is:S_5 = 5/2 * (5 + 25) = 75. This formula allows for the quick calculation of the total sum for any number of terms within the sequence. -
Relationship to Multiples of 5: The sequence is fundamentally linked to multiples of 5. Each term is a multiple of 5, highlighting its inherent divisibility and relationship to the number 5 itself. This connection opens up avenues for exploration concerning divisibility rules, prime factorization, and other number theoretical concepts.
Applications in Different Fields
While seemingly simple, the principles embodied in the sequence 5, 10, 15, 20, 25 find applications in various fields:
-
Computer Science: Arithmetic progressions are fundamental in computer science, particularly in algorithms involving loops and iterations. The sequence can model scenarios such as incrementing counters, processing data in batches, or scheduling tasks at regular intervals.
-
Physics: In physics, many physical phenomena exhibit uniform change over time. For instance, an object falling under constant gravity displays a linear increase in velocity, which can be modeled using an arithmetic progression. Similarly, concepts like uniformly accelerated motion rely on the principles of arithmetic progression for mathematical description and prediction.
-
Finance: In finance, arithmetic progressions can be used to model scenarios such as constant annual investment growth (with no compounding), regular payments on a loan, or the projected growth of a company's revenue under a specific linear growth model. Though simpler models, they offer a starting point for more sophisticated financial modeling.
-
Engineering: In engineering design and construction, arithmetic progressions find applications in tasks like calculating the evenly spaced placement of structural supports or the uniform distribution of loads along a beam. These are simplified applications but illustrate the sequence's underlying power.
-
Music: The sequence can be creatively applied in musical composition. For instance, it could represent note durations, rhythmic patterns, or even melodic intervals. The repetitive nature of the progression could create a sense of regularity or contrast, depending on its context within the musical piece.
Exploring the Creative Potential
Beyond its mathematical significance, the sequence 5, 10, 15, 20, 25 holds creative potential:
-
Visual Arts: The sequence can inspire artistic endeavors. Imagine a visual artwork where the size, spacing, or color intensity of elements increases according to the sequence. This could lead to a visually engaging piece exploring concepts of growth, progression, or repetition.
-
Literature: The sequence could be woven into a narrative as a recurring motif, symbolizing progress, growth, or a cyclical pattern within the story. Its regularity could offer a sense of predictability or irony, depending on the context.
-
Music Composition: As mentioned earlier, the sequence could be employed to structure musical phrases, rhythms, or melodic patterns. The sequence's simple mathematical structure can be creatively juxtaposed with more complex musical ideas.
-
Game Design: The sequence could be used to structure game levels, score progression, or resource acquisition. The predictability of the sequence could create a sense of steady progression, whereas deviations from the pattern could add elements of surprise or challenge.
-
Poetry: The sequence could inspire poetic forms or rhythmic patterns, possibly reflecting themes of order, growth, or the passage of time.
Frequently Asked Questions (FAQs)
Q1: Are there any other sequences similar to 5, 10, 15, 20, 25?
A1: Yes, infinitely many. Any arithmetic progression with a constant difference will share similar properties. For example, 2, 4, 6, 8, 10 (common difference 2) or 7, 14, 21, 28, 35 (common difference 7) are examples. The key is the constant difference between successive terms.
Q2: How can I find the 100th term in this sequence?
A2: Using the general formula a_n = 5n, simply substitute n = 100: a_100 = 5 * 100 = 500. The 100th term in the sequence is 500.
Q3: What if the common difference wasn't constant? Would it still be an arithmetic progression?
A3: No. A non-constant difference would indicate a different type of sequence, possibly a geometric progression (where terms are multiplied by a constant), a Fibonacci sequence, or some other pattern. The constant difference is defining for arithmetic progressions.
Q4: Can this sequence be extended infinitely?
A4: Yes, an arithmetic progression can be extended infinitely in both directions. We can continue adding terms indefinitely by repeatedly adding the common difference (5), and we can also theoretically extend it backwards (0, -5, -10, etc.) although the practical applications might be limited depending on the context.
Conclusion: A Simple Sequence with Profound Implications
The sequence 5, 10, 15, 20, 25, while appearing deceptively simple, provides a gateway to understanding fundamental mathematical concepts and exploring their connections to diverse fields. Its inherent properties – the common difference, the general formula, and the sum of the series – allow for prediction, extrapolation, and application in various contexts. From computer science and physics to finance, engineering and the arts, the underlying principles of this arithmetic progression find practical and creative applications. By exploring this sequence, we gain a deeper appreciation for the beauty and power of mathematics and its profound influence on the world around us. The seeming simplicity of this progression belies a rich tapestry of connections and potential that extends far beyond its initial appearance. Further exploration into arithmetic sequences and their various applications will reveal even more of their fascinating properties and usefulness.
Latest Posts
Latest Posts
-
Convertidor De Millas En Km
Sep 15, 2025
-
Convert 175 C To Fahrenheit
Sep 15, 2025
-
110 Cm In Waist Size
Sep 15, 2025
-
Convert 65 Inches To Feet
Sep 15, 2025
-
How Tall Is 64 Cm
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 5 10 15 20 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.