6 12 18 24 30
pachranga
Sep 11, 2025 · 5 min read
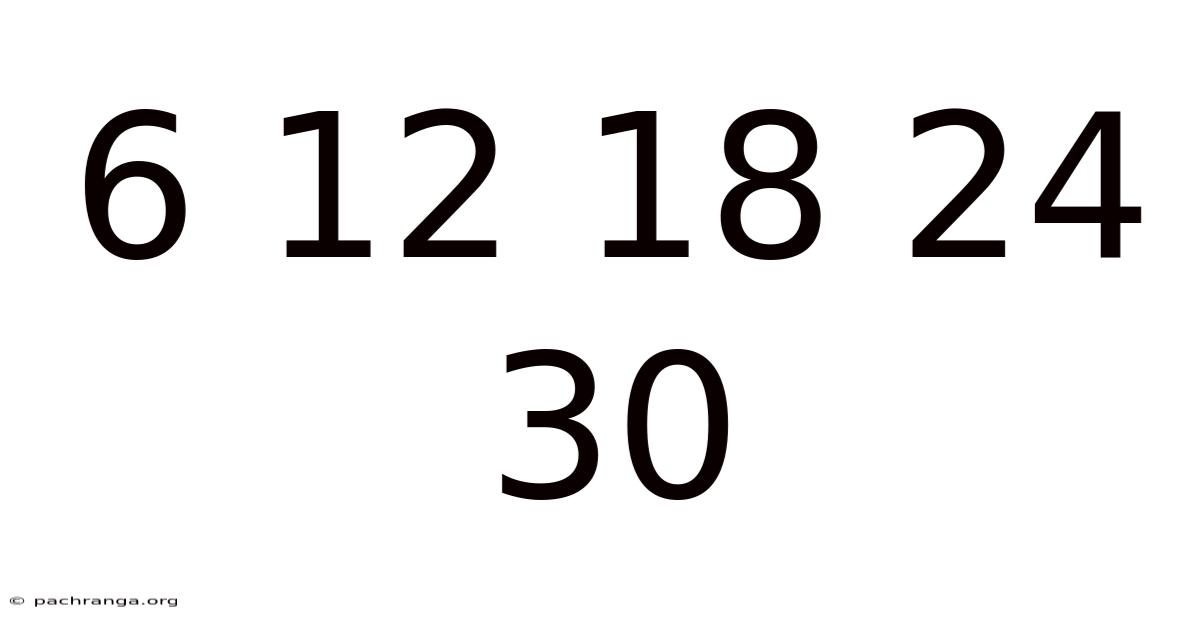
Table of Contents
Unveiling the Secrets Behind the Sequence: 6, 12, 18, 24, 30... and Beyond
This article delves into the seemingly simple sequence: 6, 12, 18, 24, 30… At first glance, it might appear straightforward, but a closer examination reveals a world of mathematical concepts and applications, from basic arithmetic to advanced number theory. We'll explore the pattern, its underlying principles, different ways to represent it, and its relevance in various fields. Understanding this sequence provides a foundation for grasping more complex mathematical relationships and problem-solving strategies.
Identifying the Pattern: A Simple Arithmetic Progression
The most obvious characteristic of the sequence 6, 12, 18, 24, 30… is its consistent increase. Each subsequent number is obtained by adding 6 to the previous one. This consistent addition of a fixed value defines an arithmetic progression (AP). In an AP, the difference between consecutive terms remains constant. This constant difference is known as the common difference, denoted by 'd'. In our sequence, the common difference (d) is 6.
- 6 + 6 = 12
- 12 + 6 = 18
- 18 + 6 = 24
- 24 + 6 = 30
This simple pattern allows us to easily predict the next terms in the sequence. By continuing to add 6, we can extend the sequence indefinitely: 36, 42, 48, and so on. This predictability is a fundamental property of arithmetic progressions and makes them easily manageable in mathematical calculations.
Representing the Sequence: Formulas and Generalizations
The consistent pattern of an arithmetic progression allows us to represent the sequence using a general formula. This formula enables us to find any term in the sequence without having to calculate all the preceding terms. The general formula for the nth term of an arithmetic progression is:
a<sub>n</sub> = a<sub>1</sub> + (n - 1)d
Where:
- a<sub>n</sub> represents the nth term in the sequence.
- a<sub>1</sub> represents the first term in the sequence (in our case, 6).
- n represents the position of the term in the sequence (1st, 2nd, 3rd, etc.).
- d represents the common difference (in our case, 6).
Let's use the formula to find the 10th term (a<sub>10</sub>) in our sequence:
a<sub>10</sub> = 6 + (10 - 1) * 6 = 6 + 54 = 60
Therefore, the 10th term in the sequence is 60. This formula provides a powerful tool for working with arithmetic progressions, allowing for efficient calculation of any term without manually extending the sequence.
Beyond the Basics: Exploring the Factors and Multiples
The sequence 6, 12, 18, 24, 30… is not just an arithmetic progression; it's also a sequence of multiples of 6. This observation opens up a whole new perspective, connecting our sequence to the concepts of factors and multiples in number theory.
- 6 = 6 x 1
- 12 = 6 x 2
- 18 = 6 x 3
- 24 = 6 x 4
- 30 = 6 x 5
This means each number in the sequence is divisible by 6, making 6 a common factor for all terms. This property allows us to express the sequence as:
a<sub>n</sub> = 6n
This simpler formula directly relates the term number (n) to the value of the term (a<sub>n</sub>). This representation highlights the intimate connection between the sequence and the concept of multiples. It's a more concise and insightful representation than the general arithmetic progression formula in this specific case.
Applications in Real-World Scenarios
Arithmetic progressions, and specifically sequences like 6, 12, 18, 24, 30…, have numerous applications in various fields:
- Financial Calculations: Calculating compound interest, loan repayments, or savings growth often involves arithmetic progressions.
- Physics: Analyzing uniformly accelerated motion, where velocity changes consistently over time, utilizes arithmetic progressions.
- Computer Science: Certain algorithms and data structures involve sequences with a constant difference.
- Engineering: Calculating the dimensions of structures or the progression of materials can utilize arithmetic progressions.
- Everyday Life: Counting objects arranged in rows or columns with a consistent increment, such as arranging chairs in a hall, or stacking boxes.
Further Explorations: Beyond the Arithmetic Progression
While the arithmetic progression aspect of the sequence is prominent, it's essential to explore potential extensions and variations:
- Geometric Progression: While this sequence is not a geometric progression (where each term is multiplied by a constant), one could create a related geometric progression using the same starting number. For example, 6, 18, 54, 162… is a geometric progression with a common ratio of 3.
- Fibonacci Sequence: Although unrelated at first glance, exploring the relationship between our sequence and the Fibonacci sequence (1, 1, 2, 3, 5, 8…) could uncover interesting mathematical relationships through advanced number theory.
- Prime Numbers: Investigating the prime factorization of each number in the sequence could reveal patterns in the distribution of prime factors.
Frequently Asked Questions (FAQ)
Q: What is the 20th term in the sequence 6, 12, 18, 24, 30…?
A: Using the formula a<sub>n</sub> = 6n, the 20th term (a<sub>20</sub>) is 6 * 20 = 120.
Q: Is this sequence a geometric progression?
A: No, this sequence is an arithmetic progression because there's a constant difference between consecutive terms, not a constant ratio.
Q: Can this sequence be represented in other ways besides an arithmetic progression?
A: Yes, as shown above, it can be represented as a sequence of multiples of 6 (a<sub>n</sub> = 6n), which is a more concise representation in this specific case.
Q: What are some real-world examples of this type of sequence?
A: Examples include the total cost of items priced equally, the distance covered during uniformly accelerated motion, or the growth of savings with consistent additions.
Conclusion: The Power of Simple Sequences
The sequence 6, 12, 18, 24, 30… appears simple at first, but a deeper investigation reveals the underlying principles of arithmetic progressions, factors, and multiples. Understanding these concepts provides a valuable foundation for more complex mathematical explorations. The ability to identify patterns, develop formulas, and apply them to real-world scenarios is a critical skill in various fields, highlighting the power and relevance of seemingly simple mathematical sequences. This sequence, therefore, acts as a gateway to a broader understanding of mathematical structures and their applications. Further exploration into related mathematical concepts will undoubtedly reveal even more fascinating connections and applications.
Latest Posts
Latest Posts
-
189 Grados Centigrados A Fahrenheit
Sep 11, 2025
-
Differences Between Bsl And Asl
Sep 11, 2025
-
1kg Bang Bao Nhieu Pound
Sep 11, 2025
-
155 Degrees Fahrenheit To Celsius
Sep 11, 2025
-
How Much Is 170 Cm
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 6 12 18 24 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.