6 394 Divided By 42
pachranga
Sep 14, 2025 · 5 min read
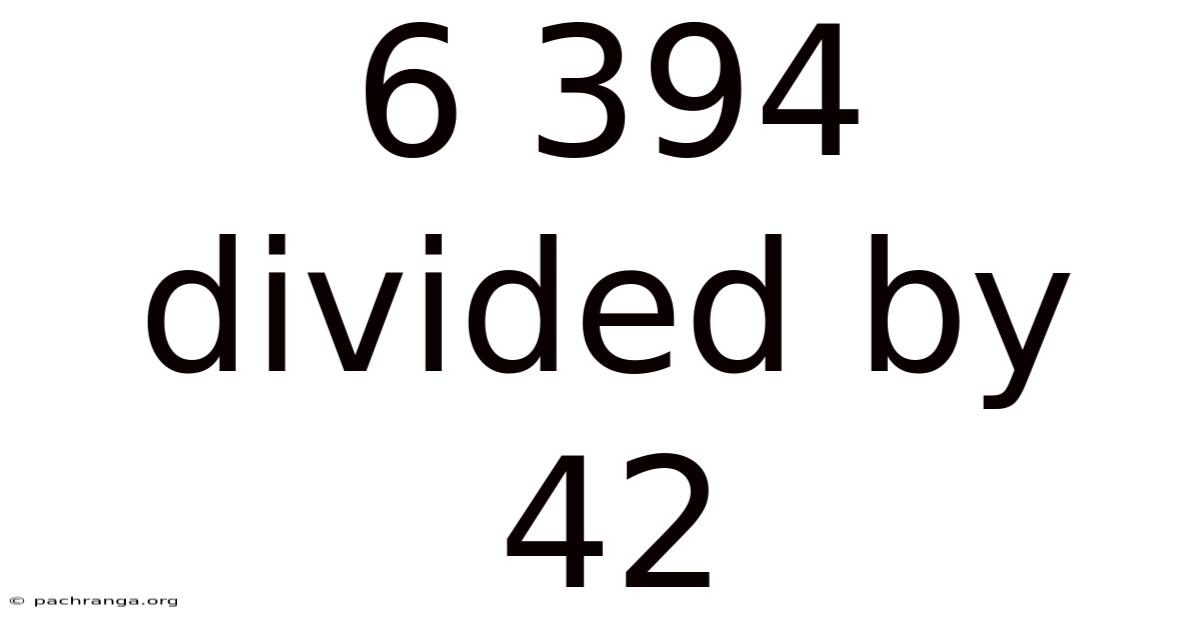
Table of Contents
Unveiling the Mystery: A Deep Dive into 6394 Divided by 42
Dividing 6394 by 42 might seem like a simple arithmetic problem, something easily tackled with a calculator. But let's go beyond the immediate answer and explore the underlying concepts, different methods of solving this division problem, and delve into the broader mathematical principles involved. This comprehensive guide aims to illuminate not just the solution but the why behind it, fostering a deeper understanding of division and its applications. This article will cover various approaches, from the traditional long division method to alternative strategies, ensuring a thorough and engaging learning experience.
Understanding the Problem: 6394 ÷ 42
The problem, 6394 divided by 42 (written as 6394 ÷ 42 or 6394/42), asks: "How many times does 42 fit into 6394?" The answer will represent the quotient, while any remaining amount will be the remainder. This seemingly simple question opens the door to a rich exploration of mathematical processes and their applications in various fields.
Method 1: Long Division – The Classic Approach
Long division is a fundamental arithmetic operation used to divide large numbers. Let's work through 6394 ÷ 42 step-by-step:
-
Set up the problem: Write 6394 inside the long division symbol (⟌) and 42 outside.
-
Divide the first digits: How many times does 42 go into 63? It goes in once (1 x 42 = 42). Write "1" above the 3 in 6394.
-
Subtract: Subtract 42 from 63: 63 - 42 = 21.
-
Bring down the next digit: Bring down the next digit (9) from the dividend (6394) to form 219.
-
Repeat the process: How many times does 42 go into 219? It goes in five times (5 x 42 = 210). Write "5" above the 9 in 6394.
-
Subtract again: Subtract 210 from 219: 219 - 210 = 9.
-
Bring down the last digit: Bring down the last digit (4) to form 94.
-
Final division: How many times does 42 go into 94? It goes in twice (2 x 42 = 84). Write "2" above the 4 in 6394.
-
Final subtraction and remainder: Subtract 84 from 94: 94 - 84 = 10. This is the remainder.
Therefore, 6394 ÷ 42 = 152 with a remainder of 10. This can be written as 152 R 10 or 152 + 10/42.
Method 2: Estimation and Adjustment
This method involves making educated guesses and refining them until you reach the correct answer. It's a great way to build number sense and mental math skills.
-
Round the divisor: Round 42 to 40 for easier mental calculation.
-
Estimate the quotient: How many times does 40 go into 6394? A rough estimate is around 150 (40 x 150 = 6000).
-
Adjust the estimate: Since we rounded down, our estimate is likely a little low. Let's try 151, 152, and so on.
-
Refine through multiplication: Multiply 42 by 152: 42 x 152 = 6384. This is close to 6394.
-
Calculate the remainder: Subtract 6384 from 6394: 6394 - 6384 = 10.
This method arrives at the same answer: 152 with a remainder of 10.
Method 3: Using a Calculator
While calculators provide a quick solution, understanding the underlying principles is crucial. A calculator directly yields the result 152.190476..., demonstrating that the exact answer is a decimal number. The remainder of 10 from the long division represents the fractional part of this decimal.
The Significance of Remainders
The remainder (10 in this case) indicates that after fitting 42 into 6394 as many times as possible (152 times), there are 10 units left over. Remainders are important in many real-world scenarios. For instance, if you're dividing 6394 candies equally among 42 children, each child gets 152 candies, and there are 10 candies left over.
Understanding Decimal Representation
The calculator's answer (152.190476...) shows the division expressed as a decimal. The decimal portion represents the remainder as a fraction of the divisor. To convert the remainder 10 to a decimal, divide 10 by 42: 10/42 ≈ 0.238. Adding this to the whole number quotient (152) gives us approximately 152.238.
Applications of Division in Real Life
Division is a fundamental operation used extensively in various fields:
- Finance: Calculating per-unit costs, dividing profits among partners, determining interest rates.
- Engineering: Dividing materials for construction, calculating ratios and proportions in design.
- Science: Determining averages, calculating concentrations, analyzing experimental data.
- Everyday Life: Sharing items equally, calculating unit prices, measuring quantities.
Further Exploration: Prime Factorization
To further enhance understanding, let's examine the prime factorization of both the dividend (6394) and the divisor (42).
- Prime factorization of 42: 2 x 3 x 7
- Prime factorization of 6394: 2 x 7 x 456 + 2
This analysis provides insight into the divisibility of the numbers and can help in simplifying calculations in certain situations, particularly when dealing with fractions.
Frequently Asked Questions (FAQ)
Q1: What if I want to express the answer as a fraction?
A1: The answer can be expressed as a mixed number: 152 10/42. This can be simplified further by finding the greatest common divisor (GCD) of 10 and 42, which is 2. Simplifying the fraction gives 152 5/21.
Q2: Are there other methods to solve this division problem?
A2: Yes, iterative methods, using software or programming, or even employing specialized algorithms for efficient division (especially for extremely large numbers) could be used.
Q3: What is the importance of understanding different methods of division?
A3: Understanding different methods enhances problem-solving skills, builds number sense, and promotes deeper comprehension of mathematical concepts. It allows you to choose the most appropriate method depending on the context and available tools.
Q4: Can a remainder be larger than the divisor?
A4: No. If the remainder is larger than the divisor, it means the division was not performed correctly. The remainder must always be smaller than the divisor.
Conclusion: Beyond the Numbers
This exploration of 6394 divided by 42 has extended beyond a simple arithmetic calculation. We've delved into the underlying principles of long division, explored alternative approaches, analyzed the significance of remainders and decimal representations, and touched upon the broader applications of division in real-world contexts. The goal was not merely to find the answer (152 with a remainder of 10 or approximately 152.238) but to cultivate a deeper and more intuitive understanding of this fundamental mathematical operation. Remember, the true power lies not just in getting the right answer, but in understanding the process of arriving at it. This understanding forms the foundation for more advanced mathematical concepts and problem-solving abilities.
Latest Posts
Latest Posts
-
What Is 165 In Kilograms
Sep 14, 2025
-
43 Degrees Fahrenheit In Celsius
Sep 14, 2025
-
13c Is What In Fahrenheit
Sep 14, 2025
-
How Large Is 1 8 Cm
Sep 14, 2025
-
How Much Is 130 Cm
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 6 394 Divided By 42 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.