What's 1.25 As A Fraction
pachranga
Sep 17, 2025 · 5 min read
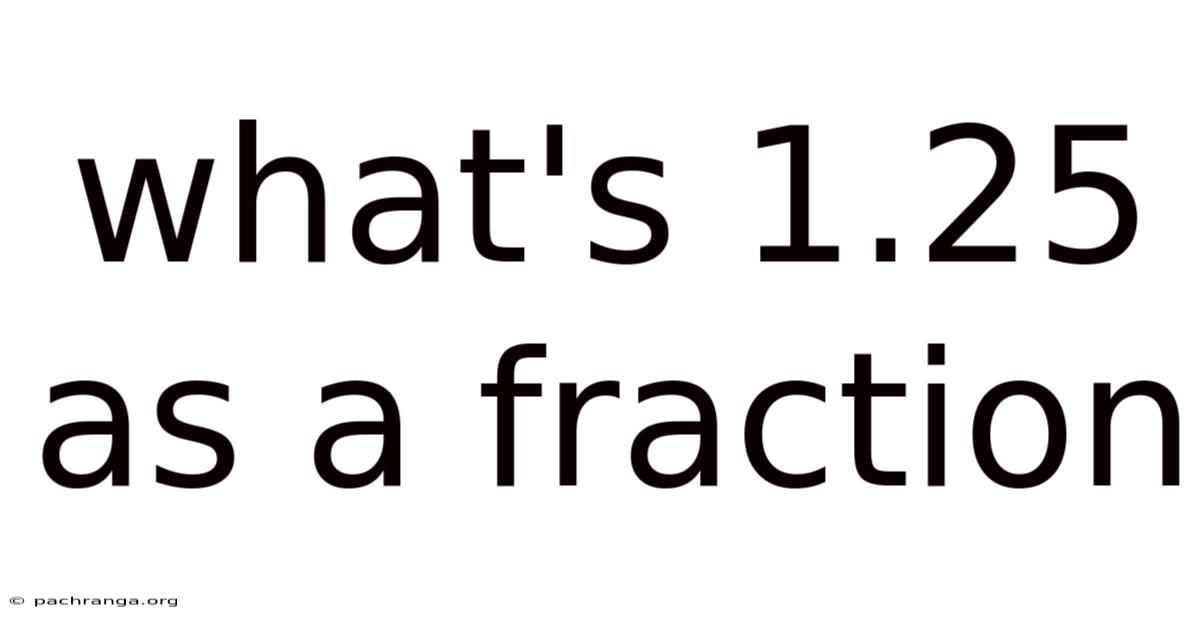
Table of Contents
What's 1.25 as a Fraction? A Comprehensive Guide
Understanding decimal-to-fraction conversions is a fundamental skill in mathematics. This comprehensive guide will explore how to convert the decimal 1.25 into a fraction, explaining the process step-by-step and delving into the underlying mathematical principles. We'll cover various methods, address common misconceptions, and answer frequently asked questions to provide a complete understanding of this essential concept. This will be useful for students, educators, and anyone looking to improve their math skills.
Understanding Decimals and Fractions
Before we dive into the conversion, let's briefly review the concepts of decimals and fractions. A decimal is a number expressed in the base-10 numeral system, using a decimal point to separate the integer part from the fractional part. For example, 1.25 has an integer part of 1 and a fractional part of 0.25.
A fraction, on the other hand, represents a part of a whole and is expressed as a ratio of two integers, the numerator (top number) and the denominator (bottom number). For example, 1/2 represents one-half. The denominator indicates the number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
Method 1: Using the Place Value System
This is the most straightforward method for converting a decimal to a fraction. We analyze the place value of each digit after the decimal point.
-
Identify the place value of the last digit: In 1.25, the last digit, 5, is in the hundredths place (two places after the decimal point).
-
Write the decimal as a fraction with a denominator based on the place value: Since the last digit is in the hundredths place, the denominator will be 100. The numerator will be the digits after the decimal point, without the decimal point: 25. Therefore, 0.25 can be written as 25/100.
-
Combine the whole number and the fraction: Since the original number is 1.25, we add the whole number 1 to the fraction: 1 + 25/100.
-
Convert to an improper fraction (optional): To express the number as a single fraction, we convert the mixed number into an improper fraction. To do this, we multiply the whole number by the denominator and add the numerator, then place this result over the original denominator: (1 * 100) + 25 / 100 = 125/100
Therefore, 1.25 as a fraction is 125/100.
Method 2: Simplifying the Fraction
The fraction 125/100 is not in its simplest form. To simplify a fraction, we find the greatest common divisor (GCD) of the numerator and the denominator and divide both by it. The GCD of 125 and 100 is 25.
Dividing both the numerator and the denominator by 25, we get:
125 ÷ 25 = 5 100 ÷ 25 = 4
Therefore, the simplified fraction is 5/4.
Method 3: Using Equivalent Fractions
This method involves finding an equivalent fraction by multiplying or dividing both the numerator and denominator by the same number. While not as direct as the previous methods, it demonstrates an important principle in working with fractions. Starting with 125/100, we can repeatedly divide both the numerator and denominator by common factors until we reach the simplest form.
- Divide by 5: 125/100 = 25/20
- Divide by 5 again: 25/20 = 5/4
Understanding the Result: 5/4
The simplified fraction 5/4 is an improper fraction because the numerator (5) is larger than the denominator (4). This indicates a value greater than 1. We can convert this improper fraction to a mixed number by dividing the numerator by the denominator:
5 ÷ 4 = 1 with a remainder of 1.
This means 5/4 is equal to 1 and 1/4, which is consistent with our original decimal, 1.25.
The Importance of Simplification
Simplifying fractions is crucial for several reasons:
- Clarity: A simplified fraction is easier to understand and work with.
- Accuracy: Working with simplified fractions reduces the risk of errors in calculations.
- Standardization: Simplifying fractions ensures that results are presented in a consistent and universally accepted format.
Common Mistakes to Avoid
- Incorrect place value identification: Carefully determine the place value of the last digit in the decimal.
- Errors in simplification: Ensure that you find the greatest common divisor (GCD) to simplify the fraction fully.
- Forgetting the whole number: When converting a decimal greater than 1, remember to include the whole number part in the fraction.
Frequently Asked Questions (FAQ)
Q: Can I convert any decimal to a fraction?
A: Yes, any terminating or repeating decimal can be expressed as a fraction. Non-repeating, non-terminating decimals (like pi) cannot be expressed as a simple fraction.
Q: What if the decimal has more digits after the decimal point?
A: The process remains the same. For example, to convert 2.345 to a fraction:
- The last digit (5) is in the thousandths place, so the denominator will be 1000.
- The numerator will be 345.
- The mixed number is 2 and 345/1000.
- Simplify the fraction by finding the GCD of 345 and 1000 (which is 5) to get 69/200.
Q: Why is simplifying important?
A: Simplifying makes the fraction easier to use in calculations and comparisons. It's the mathematical equivalent of reducing a fraction to its lowest terms.
Conclusion
Converting decimals to fractions is a fundamental skill in mathematics. Understanding the place value system and the process of simplification is essential for accurate and efficient conversion. By following the methods outlined in this guide, you can confidently convert any decimal into its fractional equivalent and improve your overall mathematical understanding. Remember to always simplify your fraction to its lowest terms for clarity and accuracy. Practice makes perfect, so try converting various decimals to fractions to reinforce your understanding of this important concept.
Latest Posts
Latest Posts
-
171cm To Inches And Feet
Sep 17, 2025
-
37 3 C To F
Sep 17, 2025
-
83 3 4 Divided By 2
Sep 17, 2025
-
Whats 165 Cm In Feet
Sep 17, 2025
-
180 Centigrade Equals What Fahrenheit
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What's 1.25 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.